預測
讓我們暫停一下,來看看大多數交易商和投資者都會遇到的一個陷阱,預測陷阱。稍微考慮一下期望收益的觀念就能讓我們更清楚地看到,為什么有那么多人那么多年以來都會在預測市場或者股票未來趨勢時遇到挫折。他們都把預測的運算法則建立在過去的基礎上,有些時候甚至認為它會重現。然而,這樣一種急于求成的預測甚至可能導致你所有資本的虧損.怎么會這樣呢？因為你可能在用一個有90％正確率但仍會虧掉所有錢的交易方法。
考慮一下以下這個“系統”。它有90％的盈利交易和10％的虧損交易；盈利交易的平均額是275美元,虧損交易的平均額是2700美元,那么期望收益= 0. 9*275—0．1 *2700= -22．5 即期望收益是負的。這是一個有90％時間正確的系統．但你最終卻虧掉了所有的錢。在我們的投資中存在著一種非常強烈的想要正確的心理偏向。對于大多數人來說,這個偏向極度無視我們方法的總體目標是想要獲得利潤,或者說它阻礙了我們達到真正的潛在利潤。大多數人有壓倒一切的、想要控制市場的欲望,因此,最后是以市場控制他們而告終。
現在你應該很清楚了,是回報和機會的結合才能讓你確定一種方法是有效的還是無效的。在確定一個系統或方法的相對價值時,你還必須考慮一下因素（4）,就是你多久能玩一次游戲。

6．4 期望收益和R乘數

到目前為止, 我們都是在玩捉球游戲。在每個彈球袋子中,我們知道彈球的總數,每個彈球被抓出的幾率和它的回報。但當我們在市場中處理系統產生的交易時,這些就沒有一個是真的了。
當你參與到市場中時,并不知道贏或虧的確切幾率。此外,你也不知道確切地會贏取或者虧損多少。然而,你可以作歷史測試從而對期望收益有個概念。你也可以從實時交易或投資中得到大量的數據樣本,使用這些樣本就可以知道系統的大體期望收益是多少。為了弄清楚每次交易的風險回報率和它發生的頻率,必須進行單個交易的郵資。在徹底做完這個練習后,你會對所使用方法的真實特性有一個更好的了解。
如果你完全是一個隨意的、沒有系統性的交易商．那么就可以回顧一下過去的交易結果。思考一下自己是怎么賺錢或者虧損的。你可以遵照我們將要介紹的類似的步驟,在一組或者一股的基礎上重新考慮一下做過的每次交易。弄清你每次交易的風險（就是初始離市點）和收盤的利潤和虧損后,就可以計算每次交易的風險回報率了。

R乘數
我把一次交易的風險回報率稱作一個“R乘數”,R僅僅是初始風險的一個表示符號。要計算一次交易的R乘數,只需在拋出該頭寸時把捕獲的點數除以初始風險就可以了。你可以簡單地使用每個合約或者每100股份額的美元價值,比如說,如果你冒險投資了500美元而獲得了1500美元的收益,那么你的R乘數就是3。圖6-1顯示了這樣一個例子,入市點是1997年8月4日的2511點,該系統使用了一個等于104點的3倍于平均實際價格幅度的止損。因此．初始離市點是2511-104,等于2407點。該系統最終于1997年9月29日在3O69點時離市。并巨獲得了558點的利潤。由于初始風險（1R）是104點,最后利潤是558點,那么利潤就是一個5.37R乘數。不管是盈利還是虧損,對所有的交易都可以這樣計算。只不過虧損的交易是一個負的R乘數。

很多構成歷史性的模擬或者先前交易結果的不同R乘數是你期望收益的組成部分。這些R乘數的本質特性將會完全決定你所用方法的全部期望收益。它有助于你確定正確的財務管理法則,并應用到交易方法中去,以達到你所有的目標。說到R乘數的本性,我指的是大小、頻率和不同R乘數的順序。
試想,把系統的交易當作只是一些R乘數。然后假設每次交易只是簡單地從一個袋里掏出的一個彈球。一旦你撈出了這個彈球后,就能確定它的R乘數,然后再把它放回到袋里。
玩這個游戲的時候．你需要開發一個有助于你利用期望收益的頭寸調整運算法則。另外,你還希望該法則與每次交易的初始風險和正在進行中的賬戶資本有一定的相關性。對初涉者來說．可以考慮一個風險百分率運算法則,依據它來連續投資當前賬戶資本的一個固定百分比、這種頭寸調整運算法則基本上就表示這個1R風險是相同的,而不管什么時候用它或者用在哪種股票或市場上。這是因為你的頭寸大小一直是你資本的一個固定的百分比（比如說1％）,而無論初始風險（R）有多大。請參見第12章。
此外,你想考慮一下被抓出來的彈球的可能分布,也就是順序系統的盈利百分比與一連串的虧損交易的長度成反比,因此、你需要一個頭寸調整的運算法則,以使你能撤出可能的一連串虧損交易并仍然能利用大的盈利進行交易。
很多交易商未能利用健全的系統進行交易。這是因為：
（1 ）他們沒有以他們的方法為市場帶給他們的交易分布做好準備。
（2）他們過度使用了杠桿作用或投資不足。給定了系統的盈利幾率后,你就可以估計1000次試驗中可能的最大連續虧損交易數,但是你無法真正知道“確定的”值。例如,即使是拋硬幣也可能多次產生正面朝上的情況。

圖6－2顯示了一個類似表6l捉球游戲的機會因素為60的樣本的交易分布。注意一下第46次和第55次交易之間一連串長期的虧損交易。直到此時,很多玩此游戲的人才漸漸總結出以下規則：
（1）確定將要被抓出來的盈利彈球的時間；
（2）決定在游戲中的某一未來時刻以違反期望收益的方式下賭,因此,他們從中獲得了收益。如果這一連串的虧損在游戲中恰好發生得較早,那么第（2）比較適用。如果這一連串的虧損在游戲中恰好發生得較晚,則第（1 條更適用些。有些參加者的心理迫使他們交易虧損越多。下的賭注越大,因為他們“認為”一次盈利就“躲在某一角落里”。我確信你能夠猜出這樣一個游戲的一般結果。

圖6-3顯示了對上述游戲每次以當前資本的固定百分比下注的資本曲線。固定百分比是 1%,1.5%,2% 。賭注為1%的60次實驗的回報率是40.7%,并且從最高點到最低點的下跌量是12。3%,交易5、6和10各有一連串明顯的虧損。

圖6-4顯示了以違反期望收益的當前資本的1。0％為賭注的資本曲線,你有64％的機會是正確的,甚至還可能享受一連串為數達10次的盈利交易,但你卻會虧損起始資本的37％。
如果你想更好地了解這個系統是如何工作的．可能至少需要評估10倍以上次交易。到那時才能做出一個更好的關于頭寸調整（這里是賭注調整）的運算法則并確定杠桿水平。此外,我們還能夠測試一下此系統在未來交易中的作用。
我們可以對能設想到的、將來可能發生的很多情形進行心理演練的培養,就是訓練我們在那種情形發生時應該做出的反應。記住,即使是這樣你也并不能確切知道這個彈球袋或者市場將會表現出什么結果。這就是為什么你的心理演練過程應包括一部分訓練自己怎樣對突發事件做出反應的內容。
產生了103次交易,其中有60次是虧損的,占58.3％,有43次是盈利的,占41.7％。交易的分布如表6－2所示．每次交易僅交易一個單位．也就是最小頭寸大小的交易。那么,總利潤=54137美元 總損失=43304美元凈利潤=10833美元

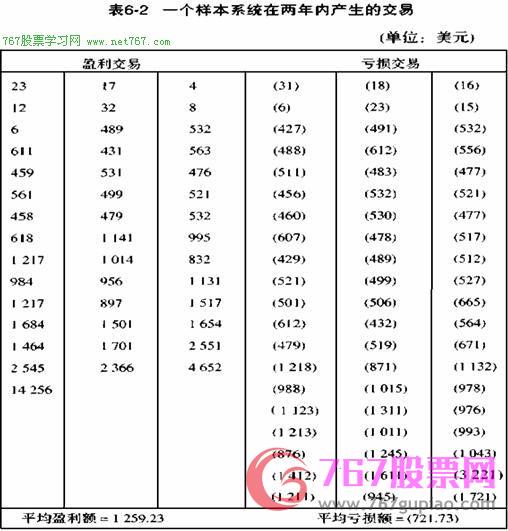
從表中我們可以計算出期望收益=0.417 *＄1259.23-0.583 *＄721.73＝＄525.10- ＄420.77＝＄104.33 顯然,當你有了數據樣本后,就同樣能夠得出凈利潤,然后把它除以交易的次數就可以得到期望收益。